Matematika Kreatif dan Solutif

Pada tulisan sebelumnya, ada latihan soal yang digunakan untuk melatih konsep yang dijelaskan dalam tulisan tersebut. Ini dia soalnya

Mari kita bahas solusi dari soal tersebut. Soal ini sebenarnya tidak hanya melatih kita untuk memikirkan solusi dari hal yang sederhana, tapi juga untuk berfikir kreatif dan solutif. How can? Let’s check it out :)

Seperti hint yang sudah diberi sebelumnya, kita akan menggunakan garis AF sebagai garis bantu. Namun, pertanyaan berikutnya muncul, mengapa harus pakai AF sebagai garis bantu? Pertanyaan yang bagus. Nah, disinilah sebenarnya salah satu hal unik dari pembelajaran matematika, khususnya di olimpiade. Tidak ada cara yang kaku untuk menyelesaikan sebuah permasalahan. It can be solved with this way, also in another way. Bagaimana memecahkan permasalahan itu juga berdasarkan seberapa kreatif kita dalam mencari dan mencoba langkah solusi yang mungkin dapat digunakan untuk memecahkan permasalahan tersebut. Bagaimana caranya agar kreatif? Berlatihlah dan terus berlatih dalam memecahkan permasalahan tersebut. Bukannya kita akan semakin bijak dengan banyak masalah yang dapat kita selesaikan? Cieh :D

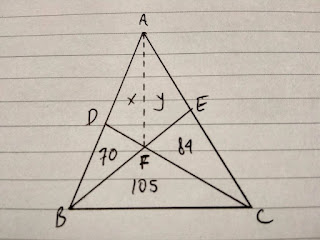
Kembali ke laptop, eh ke permasalahan tadi. Untuk mencari luas ABC, kita harus mencari luas ADFE. Dengan garis bantu AF, dimisalkan luas ADF=x dan AFE=y

Kemudian, coba kita lihat bagian segitiga AFC.

Dengan konsep di tulisan sebelumnya, dapat terlihat bahwa segitiga AFE dan segitiga EFC memiliki tinggi yang sama. Maka, perbandingan luasnya adalah

 

Dengan cara yang sama, karena segitiga ABE dan EBC juga memiliki tinggi yang sama, maka

Sehingga dapat diperoleh bahwa

Dan kemudian dengan cara yang sama, jika kita melihat bagian segitiga AFB, dapat disimpulkan bahwa:

Lalu, coba kita kerjakan dua persamaan di atas, sebagai berikut:

Maka, kemudian akan diperoleh L_ABC = 200+216+70+84+105 = 675 

Yuk, kita kembangkan kreativitas dalam belajar matematika agar dapat menyelasaikan permasalahan secara solutif. Selamat belajar matematika :)